What are the criteria for deciding the types of meshing in ANSYS?
When deciding the types of meshing in ANSYS, several criteria should be considered to ensure an appropriate mesh for accurate and efficient analysis.
The key criteria include:
Geometry: Consider the complexity and shape of the geometry. For simple geometries, structured meshing can be suitable, while for complex and irregular geometries, unstructured meshing may be more appropriate.
In geometry, the type of geometric element can be determined based on various criteria, which include:
Dimensionality: The dimension of a geometric element refers to the number of coordinates required to specify its position in space.
-
-
- A point is a zero-dimensional element. It has no size or extent and is represented by a single location in space.
- A line is a one-dimensional element. It extends infinitely in two opposite directions and is defined by at least two distinct points.
- A plane is a two-dimensional element. It extends infinitely in all directions and is defined by at least three non-collinear points or by a point and two non-parallel lines.
-
Shape and properties: Different geometric elements have distinct shapes and properties.
-
- A point has no shape and no measurable properties such as length or area. It represents a precise location.
- A line is linear and has length but no width or height. It can be straight or curved.
- A plane is a flat surface that extends infinitely in all directions. It has length and width but no height.
Relationships with other elements: Geometric elements can also be classified based on their relationships with other elements.
-
- A point can be part of a line or lie on a plane.
- A line can be contained within a plane or intersect other lines.
- A plane can intersect other planes or contain lines and points.
By considering these criteria, you can determine the type of geometric element based on its dimensionality, shape, properties, and relationships with other elements. These criteria provide a framework for classifying and understanding geometric objects in mathematical and spatial contexts.
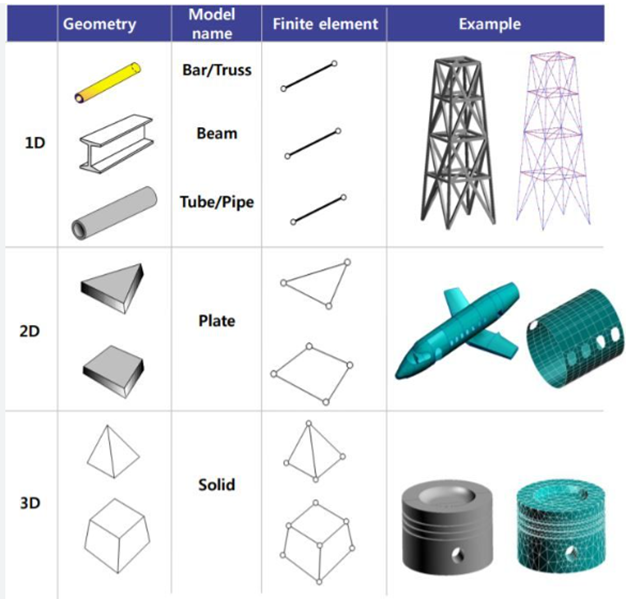
Element Types: Analyze the physical behavior of the system and select element types that can effectively represent that behavior. Based on the physical behavior analysis, choose element types that can effectively represent that behavior. ANSYS provides various element types, including:
1D Beam Elements: These elements are suitable for analyzing structures that primarily experience axial, bending, or torsional loads. Beam elements are commonly used for analyzing long, slender components like beams, trusses, and frames.
2D Shell Elements: Shell elements are ideal for modeling thin-walled structures, such as plates and shells. They can capture bending, membrane, and shear behaviors. Shell elements offer efficient modeling for structures with relatively small thickness compared to their other dimensions.
3D Solid Elements: Solid elements are used for three-dimensional analysis, representing volumetric structures. They can handle complex geometries and accurately capture stress concentrations, boundary effects, and nonlinear behaviors. Solid elements are suitable for analyzing solid components like blocks, cylinders, and irregular shapes.
Specific Purposes: Each element type serves specific purposes based on the nature of the analysis. Beam elements are appropriate for structural members subjected to axial or bending loads, shell elements are well-suited for thin structures like panels or shells, and solid elements are versatile and can handle various three-dimensional applications.
By selecting the appropriate element types in ANSYS, engineers and analysts can accurately model and simulate the physical behavior of the system under consideration, allowing for insightful analysis and informed design decisions.
Mesh Density: Determine the required level of mesh refinement based on the desired accuracy and the characteristics of the system. Regions with high stress gradients or areas of interest typically require finer meshes, while less critical regions can have coarser meshes to save computational resources.
Here are some common criteria used to decide the type of element based on mesh density:
Element Size: The size or characteristic length of the elements in the mesh can play a role in determining their type.
Fine Mesh: Elements with smaller sizes or characteristic lengths are typically used in regions where high detail or accuracy is required, such as near boundaries or regions with steep gradients.
Coarse Mesh: Elements with larger sizes or characteristic lengths can be used in regions where lower resolution is sufficient, such as areas with relatively uniform behavior or in regions of lower interest.
The choice of element type can impact the accuracy, efficiency, and stability of the numerical simulation or analysis being performed.
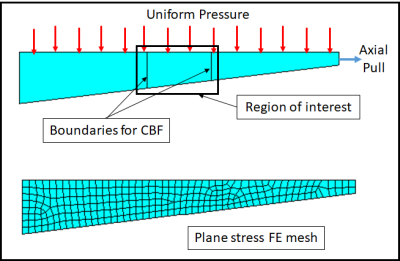
Boundary Conditions: Consider the boundary conditions and loading conditions applied to the model. Ensure that the mesh adequately captures the behavior and deformation patterns at the boundaries.
When deciding the type of element in the context of boundary conditions, the following criteria are commonly considered:
Geometry and Boundary Shape: The geometry and shape of the boundary can influence the choice of element type.
Curved Boundaries: If the boundary has curved or irregular shapes, using elements that can better approximate those shapes, such as higher-order elements or curved elements, may be more suitable.
Straight Boundaries: For boundaries with predominantly straight segments, simpler element types like linear or planar elements may be sufficient.
Displacement and Deformation: The anticipated displacement and deformation behavior at the boundary can guide the selection of element type.
Linear Elasticity: In linear elastic analysis, where small deformations are assumed, standard linear elements may be used for boundary conditions, as they can accurately capture the expected displacements and strains.
Large Deformation: In cases involving large deformations or nonlinear behavior, specialized elements such as quadratic or higher-order elements, or elements capable of handling geometric nonlinearity, may be required to accurately model the boundary conditions.
Boundary Constraints: The specific boundary constraints applied to the system can impact the choice of element type.
Fixed Constraints: If a boundary is completely fixed or restrained in a specific direction, simpler elements with appropriate degrees of freedom may be used to represent the fixed degrees of freedom accurately.
Sliding or Contact Boundaries: In cases involving sliding or contact between boundaries, special contact elements or interface elements may be utilized to model the contact behavior accurately.
Convergence criteria are typically used to assess the accuracy and reliability of numerical simulations or analyses. They guide the choice of element type in order to achieve convergence, which means obtaining stable and consistent results as the mesh is refined. Here are some convergence criteria that can influence the selection of element type:
Solution Accuracy: The desired level of accuracy in the solution is a critical criterion for convergence.
Higher-Order Elements: Higher-order elements, such as quadratic or cubic elements, can provide more accurate results compared to linear elements, especially when modeling complex phenomena or capturing detailed variations in the solution.
Element Refinement: Refining the mesh by subdividing elements into smaller sizes can enhance accuracy. This is particularly important when sharp gradients, discontinuities, or localized phenomena are present in the solution.
Solution Sensitivity: The sensitivity of the solution to local changes or perturbations can affect the choice of element type.
Element Compatibility: The chosen element type should be capable of accurately representing the sensitivity of the solution to changes in the problem conditions or boundary conditions. This ensures that the mesh refinement captures the desired sensitivity behavior.
Convergence Rate: The rate at which the solution approaches a converged state with mesh refinement can influence the choice of element type.
Rate of Convergence: Different element types may exhibit different convergence rates. It is beneficial to select an element type that converges rapidly to the desired solution, reducing the computational effort required for achieving convergence.
Solution Stability: The stability of the numerical solution and its resistance to oscillations or instabilities play a crucial role in convergence.
Stability Requirements: Some element types may possess better stability properties than others, making them more suitable for specific types of problems or solution methods. Stability considerations are particularly important when dealing with nonlinear or time-dependent phenomena.

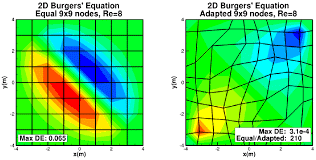
Mesh Quality: Evaluate the quality of the mesh, considering criteria such as element aspect ratio, skewness, and distortion. A high-quality mesh with well-shaped elements can improve the accuracy and stability of the analysis.
The following mesh quality criteria can guide the selection of element type:
Element Shape Regularity: The shape regularity of mesh elements is an important criterion for accurate and robust simulations.
Aspect Ratio: Elements with a low aspect ratio (ratio of the longest edge to the shortest edge) are generally preferred as they minimize shape distortion and improve solution accuracy.
Skewness: Skewness measures the deviation of an element from an ideal shape. Elements with low skewness, where the angles between adjacent edges are close to 90 degrees, are desirable for better accuracy.
Element Size and Aspect Ratio Uniformity: Uniformity in element size and aspect ratio across the mesh promotes numerical stability and convergence.
Size Ratio: Elements with similar sizes throughout the mesh minimize interpolation errors and improve solution accuracy.
Aspect Ratio Variation: Consistent aspect ratios across elements help maintain shape regularity and facilitate smoother convergence.
Orthogonality of Element Edges: Orthogonal or near-orthogonal edges between adjacent elements enhance the accuracy of numerical simulations.
Angle Deviation: Elements with edges that form angles close to 90 degrees improve the accuracy of flux calculations, especially in computational fluid dynamics (CFD) simulations.
Alignment with Geometry: The alignment of mesh elements with the underlying geometry is crucial for accurately representing the physical boundaries and features.
By considering these mesh quality criteria, engineers and analysts can make informed decisions about the type of element to use in a mesh. The goal is to choose element types that produce meshes with good shape regularity, uniformity, orthogonality, alignment with geometry, and appropriate density. These criteria contribute to accurate and reliable numerical simulations and analyses.
Computational Resources: Take into account the available computational resources, such as memory and processing power. Fine meshes require more computational resources and longer solution times. Balancing mesh density with available resources is crucial for efficient analysis.
When considering computational resources, such as memory and processing power, the choice of element type can be influenced by the following criteria:
Mesh Size and Memory Requirements:
Element Size: Finer meshes with smaller element sizes require more memory to store the mesh connectivity and solution data. If computational resources are limited, using larger element sizes can reduce memory requirements.
Mesh Density: Increasing the density of the mesh, which involves using more elements, increases the memory requirements. If memory limitations exist, a coarser mesh with larger element sizes can be chosen to reduce memory usage.
Processing Time:
Element Type Complexity: Some element types involve more computationally intensive operations, such as higher-order interpolation or more complex shape functions. Choosing simpler element types, such as linear elements, can reduce the computational time required to solve the analysis.
Solution Algorithms: Certain element types may require specific solution algorithms that have different computational complexities. For example, higher-order elements may require more complex numerical integration techniques, resulting in longer solution times.
Available Hardware and Software Capabilities:
Parallel Processing: If parallel processing capabilities are available, such as multiple processor cores or distributed computing, more computationally expensive element types can be utilized without significantly impacting solution times.
Software Compatibility: The element type should be compatible with the analysis software and the available computational libraries or modules. Some software packages may have limitations on the supported element types or may provide optimized algorithms for specific element types.
Accuracy-Resource Trade-off:
Balance between Accuracy and Resource Constraints: The element type selection should strike a balance between the desired solution accuracy and the available computational resources. Finer meshes with higher-order elements can provide more accurate results, but they may require more computational resources and longer processing times.
Iterative Analysis:
Iterative Solvers: If the analysis requires iterative solvers, the element type can impact the convergence behavior and the number of iterations needed for convergence. Choosing element types that facilitate faster convergence can help reduce computational resources.
Considering these computational resource criteria allows for the selection of an element type that optimizes memory usage, processing time, and hardware capabilities. It ensures that the analysis can be performed within the available computational resources while maintaining an acceptable level of accuracy.

Analysis Type: Different analysis types, such as structural, thermal, or fluid dynamics, may require specific meshing approaches. Consider the requirements and characteristics of the analysis type when selecting the meshing strategy.
The choice of element type in a numerical analysis is influenced by the specific type of analysis being performed. Different analysis types have unique requirements and considerations that guide the selection of element types. Here are some common analysis types and their corresponding criteria for choosing element types:
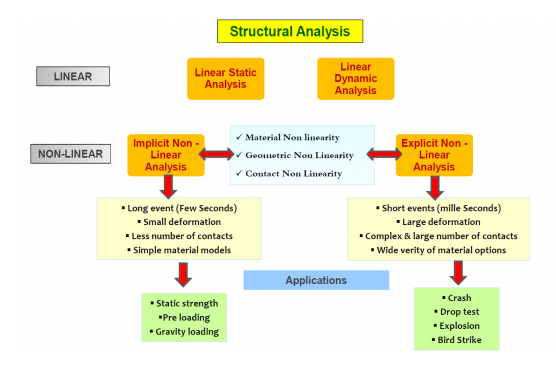
Structural Analysis:
Linear Static Analysis: For linear static analysis, standard linear elements such as linear triangles (2D) or linear tetrahedra (3D) are commonly used. These elements are sufficient for capturing linear material behavior and small deformations.
Nonlinear Analysis: Nonlinear analysis, involving large deformations or material nonlinearities, may require specialized element types such as quadratic or higher-order elements. These elements can better represent large deformations and handle nonlinear behavior.
Buckling Analysis: Buckling analysis focuses on the stability and critical loads of structures. Specialized buckling elements, such as shell or beam elements, may be appropriate to capture buckling modes and critical loads accurately.
Fluid Dynamics Analysis (CFD):
Finite Volume Method: In CFD simulations using the finite volume method, the choice of element type is typically governed by the underlying numerical discretization scheme. Typically, structured or unstructured grids consisting of various element types (triangles, quadrilaterals, tetrahedra, hexahedra) can be used based on the grid generation techniques and the specific requirements of the fluid flow problem.
Heat Transfer Analysis:
Conduction Analysis: In conduction analysis, where heat transfer is governed by thermal conduction, standard linear elements such as triangles (2D) or tetrahedra (3D) can be used effectively.
Convection or Radiation Analysis: For convection or radiation analysis, elements with appropriate properties to represent convective or radiative heat transfer, such as special boundary elements or higher-order elements, may be required.
When selecting the appropriate element type for a particular analysis type, it is essential to consider the specific requirements and behavior of the physical phenomena involved.
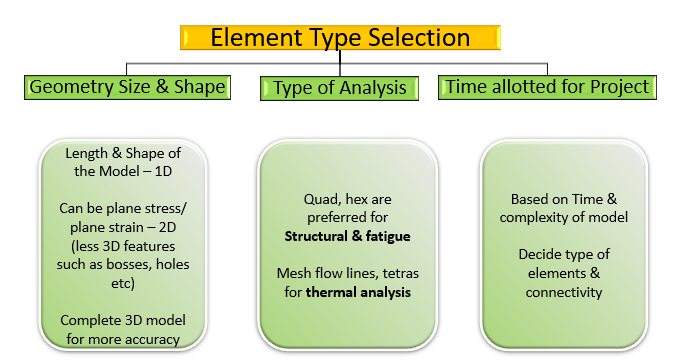
In a nut shell, once can summarize the complete element selection in a below mentioned flow chart.
Engineers can make well-informed decisions regarding meshing types in ANSYS by carefully considering these criteria. This thoughtful approach ensures accurate, reliable, and efficient analyses. Achieving optimal results involves striking a balance between mesh refinement for accuracy and computational efficiency.
To enhance their understanding of meshing techniques in ANSYS, engineers can consider enrolling in ANSYS online courses. Platforms like Artem Academy offer comprehensive online courses on ANSYS, covering topics such as element types and meshing strategies. These courses can be particularly beneficial for engineers in India, as they provide access to quality ANSYS training from the convenience of their location.
By participating in ANSYS online courses, engineers can gain insights into the selection and application of different element types within ANSYS. Additionally, they can learn about best practices for meshing, including considerations for accuracy and computational efficiency.
Through these courses, engineers can acquire the knowledge and skills required to confidently navigate ANSYS for meshing and achieve optimal results in their analyses.
.