Exploring the Versatility of 2D Element Types in Finite Element Method (FEM)
In Finite Element Analysis, the continuous domain is divided into a mesh of smaller subregions called elements, and each element is represented by a mathematical approximation referred to as a finite element. These elements are typically classified as one-dimensional (1D), two-dimensional (2D), or three-dimensional (3D), depending on the dimensionality of the problem being modeled.
Specifically, 2D finite elements are used to discretize problems that exhibit behavior primarily in two dimensions, such as plane stress, plane strain, or axisymmetric problems. They are employed when the geometry and loading conditions can be adequately represented in a two-dimensional plane, and the third dimension can be neglected or approximated as a constant value.
The shape and formulation of 2D finite elements can vary depending on the specific problem being addressed. Common types of 2D elements include triangular elements (e.g., linear or quadratic triangles) and quadrilateral elements (e.g., bilinear or biquadratic quadrilaterals). These elements are defined by a set of nodes and interpolation functions that approximate the behavior of the underlying continuous domain. The behavior of the structure or system can be analyzed, and quantities such as displacements, stresses, strains, and other relevant variables can be evaluated at specific points within each element.
Overall, 2D elements in FEM provide a powerful numerical tool for analyzing and simulating the behavior of structures and systems in two-dimensional space, enabling engineers and researchers to gain insights into the mechanical response of various physical phenomena.
Here is a detailed explanation of common types of 2D elements:
2D plane stress
2D plane stress refers to a simplified modeling approach used to analyze the behavior of a thin structure or component. It assumes that the stresses and strains within the structure are primarily confined to a single plane, neglecting the effects of stress and strain variations in the thickness direction.
When considering the thickness element in a 2D plane stress analysis, it is assumed that the thickness of the structure is much smaller compared to its other dimensions. This assumption allows for the simplification of the analysis by reducing the problem from a 3D scenario to a 2D plane, where stress and strain components vary only within that plane.
In this analysis, the structure is typically represented by a flat, two-dimensional model. The stresses and strains are assumed to vary only in the X and Y directions, while remaining constant in the Z (thickness) direction. This simplification allows for the application of two-dimensional equations of equilibrium and constitutive laws to determine the stresses, strains, and deformations within the structure.
It is important to note that the 2D plane stress analysis is applicable only when the effects of stress variations in the thickness direction can be reasonably neglected.
Overall, the 2D plane stress analysis with thickness element provides a simplified approach to analyze thin structures, allowing for efficient and practical analysis while capturing the essential behavior of the system within the plane of interest.

2D plane strain
2D plane strain element is a modeling approach used to analyze the behavior of a structure or component subjected to deformation in two dimensions while assuming no strain variations in the third dimension. It is typically employed when the structure or component is much larger in the third dimension compared to its thickness or other dimensions.
The deformation and resulting strains within the structure are assumed to be primarily confined to a single plane, while negligible in the direction perpendicular to that plane. This assumption allows for simplification of the analysis by reducing the problem from a 3D scenario to a 2D plane, where strains vary only in the X and Y directions. The structure or component is typically represented by a two-dimensional model, where deformations and strains occur in the X and Y directions. The analysis involves applying two-dimensional equations of equilibrium and constitutive laws to determine the stresses, strains, and deformations within the structure.
It is important to note that the 2D plane strain analysis is suitable when the strains in the direction perpendicular to the plane of interest are relatively small or negligible. This assumption is valid for structures or components that are significantly larger in one dimension compared to the other two dimensions, such as long beams, thick plates, or deep foundations.
However, it is crucial to carefully consider the suitability of the 2D plane strain assumption for a given problem. If significant strain variations occur in the out-of-plane direction, a more comprehensive three-dimensional analysis may be necessary to accurately capture the behavior of the structure.
In summary, a 2D plane strain element is a modeling technique used to analyze structures or components subjected to deformation in two dimensions while neglecting strain variations in the third dimension. It provides a practical and efficient approach for analyzing systems with predominant deformation occurring in a single plane.
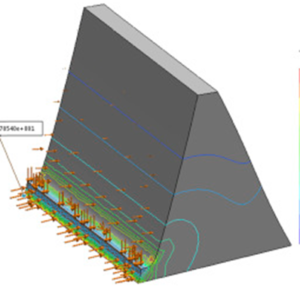
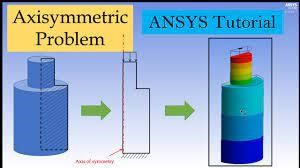
2D Axi-Symmetric
2D axisymmetric element is a modeling approach used to analyze the behavior of a structure or component that possesses rotational symmetry around a central axis. It is particularly suitable for studying cylindrical or rotationally symmetric geometries, such as pipes, pressure vessels, or circular plates.
In a 2D axisymmetric analysis, the deformation and resulting strains within the structure are assumed to be axisymmetric, meaning they vary only in the radial and axial directions. This assumption allows for a simplification of the analysis by reducing the problem from a 3D scenario to a 2D axisymmetric plane, eliminating the need to model the entire 3D volume.
The structure or component is typically represented by a 2D axisymmetric model, where deformations, strains, and stresses are computed for points along the radial and axial directions. The analysis involves applying axisymmetric equilibrium equations and constitutive laws to determine the stresses, strains, and deformations within the structure. The boundary conditions applied to the model are also axisymmetric, and the loading conditions are assumed to be symmetrical about the central axis. This allows for the consideration of rotational symmetry and simplifies the analysis process.
It is important to note that the 2D axisymmetric analysis is suitable when the geometry and loading conditions exhibit axisymmetric behavior, and the out-of-plane variations in the structure’s behavior can be reasonably neglected. However, if the structure has complex geometries or loading conditions that violate the axisymmetric assumption, a more comprehensive three-dimensional analysis may be required.
In summary, a 2D axisymmetric element is a modeling technique used to analyze structures or components with rotational symmetry around a central axis. It provides a simplified and efficient approach for studying cylindrical or rotationally symmetric geometries, enabling the analysis of behavior along the radial and axial directions while neglecting out-of-plane variations.
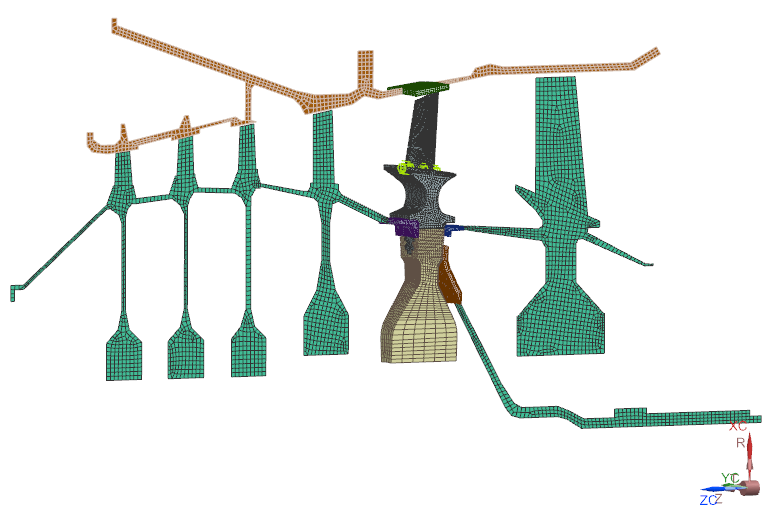
These are just a few examples of the practical applications of 2D elements for each of the type. The versatility of 2D analysis allows for the modeling and simulation of a wide range of physical phenomena, making it valuable in numerous engineering and scientific disciplines.
At Artem Academy, we offer comprehensive courses on 2D elements in Finite Element Analysis (FEA), with a specific focus on applications in engineering and scientific disciplines. Our ANSYS course delves into the practical use of 2D elements for modeling and simulating various physical phenomena.
By enrolling in our ANSYS course in India by online, students will gain an in-depth understanding of different types of 2D elements, such as triangular and quadrilateral elements. They will learn how to discretize 2D problems, including plane stress, plane strain, and axisymmetric analyses, using these elements.
Through hands-on exercises and real-world examples, students will develop the skills necessary to effectively utilize 2D elements in ANSYS software for accurate and efficient simulations. They will learn how to define element types, assign appropriate material properties, and apply boundary conditions to accurately represent the behavior of structures and systems in two dimensions.
Our experienced instructors, who possess extensive knowledge in FEA and ANSYS, will guide students through the course, providing valuable insights and practical tips for successful 2D element analysis. Upon completion of the course, students will be equipped with the expertise to tackle complex engineering problems using 2D elements and ANSYS software.
Join us at Artem Academy and elevate your understanding of 2D elements in FEA. Gain the skills needed to confidently analyze and simulate a wide range of physical phenomena, unlocking new opportunities in engineering and scientific disciplines. Enroll in our ANSYS course today and take your FEA capabilities to the next level.