The Synergistic Role of Software and Mathematics in Finite Element Analysis (FEA)
Finite Element Analysis (FEA) is a numerical method used to solve complex engineering problems by dividing them into smaller, more manageable elements. Software and mathematics play crucial roles in FEA by facilitating the analysis process.
Here’s a breakdown of their roles:
Software:
-
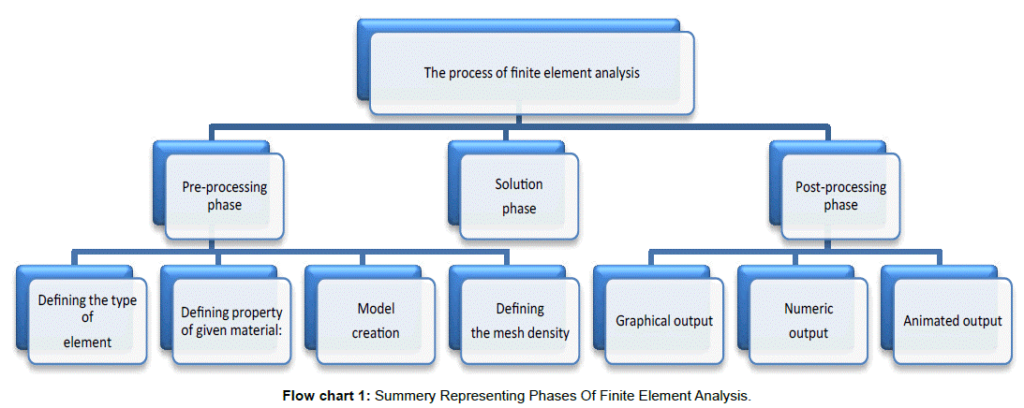
- Preprocessing: FEA software provides tools for creating and defining the geometry, applying boundary conditions, assigning material properties, and generating the finite element mesh. It allows users to set up the analysis parameters and specify the type of analysis to be performed (structural, thermal, fluid, etc.).
- Mesh Generation: FEA software automatically generates the finite element mesh by subdividing the model into smaller elements. It determines the connectivity between nodes, elements, and their relationships.
- Postprocessing: After the analysis is complete, FEA software provides postprocessing capabilities to interpret and visualize the results. Users can examine and extract important data, such as stress and deformation distributions, safety factors, mode shapes, and frequencies. This allows for the evaluation of structural performance and the identification of potential design improvements.
- Parametric Analysis: FEA software often offers parametric capabilities, allowing users to investigate the effects of varying input parameters on the structural response. This enables optimization studies and sensitivity analyses, which can aid in identifying the optimal design or operating conditions for a given structure.
- User Interface and Workflow: FEA software typically provides a user-friendly interface that allows users to interact with the software efficiently. It offers tools and menus for model setup, analysis control, result visualization, and report generation. The software’s workflow helps streamline the overall analysis process, making it easier for users to set up and execute simulations.
Overall, FEA software plays a crucial role in enabling engineers and analysts to perform accurate and efficient structural analysis. It empowers users to predict the behavior of complex systems, optimize designs, and make informed decisions based on the simulation results.
Mathematics plays a crucial role in Finite Element Analysis (FEA) by providing the mathematical foundations and techniques necessary for solving complex engineering problems. Here are some key roles of mathematics in FEA:
-
- Formulation of Governing Equations: FEA involves formulating the governing equations that describe the behavior of the analyzed structure. These equations are derived from the principles of mechanics, such as equilibrium, compatibility, and constitutive relations. Mathematics provides the tools and techniques to derive and manipulate these equations, allowing for accurate representation of the physical behavior of the structure.
- Discretization: FEA discretizes the continuous structure into smaller finite elements, each having a simpler geometry and behavior. Mathematics plays a crucial role in defining the shape functions, interpolation techniques, and numerical integration methods used to approximate the behavior of the structure within each finite element. This enables the representation of complex structures using a collection of simpler mathematical models.
- Solution Methods: FEA involves solving large systems of equations to determine the unknowns, such as displacements, stresses, and strains. Mathematics provides the numerical techniques, such as matrix algebra, numerical integration, and iterative solvers, to efficiently and accurately solve these equations. Advanced mathematical algorithms are used to handle the large-scale systems encountered in FEA, ensuring robust and reliable solutions.
- Error Estimation and Convergence: Mathematics enables the estimation of errors and the assessment of solution convergence in FEA. Through mathematical analysis, it is possible to determine the accuracy and reliability of the numerical solution, ensuring that it converges to an acceptable level of accuracy. This allows users to assess the quality of the results obtained from the FEA simulations.
- Parametric Studies and Optimization: Mathematics plays a key role in parametric studies and optimization in FEA. By varying input parameters, mathematical relationships and optimization techniques are employed to analyze the sensitivity of the structure’s response and optimize design parameters for desired performance criteria. This enables engineers to explore and optimize designs more efficiently.
Overall, mathematics provides the underlying principles, techniques, and algorithms required for the successful implementation of FEA. It enables the accurate representation, analysis, and optimization of complex structural systems, helping engineers and analysts make informed decisions and improve the design and performance of various engineering applications.
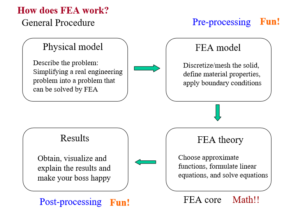
In summary, the combination of software and mathematics in FEA allows for accurate modeling and simulation of physical systems. The software provides the necessary tools and interfaces for analysis setup and execution, while mathematics provides the foundation for numerical algorithms and equations to solve the governing equations. CAE encompasses the broader field of utilizing computer software and mathematical models in engineering analysis, with FEA being a specific technique. ARTEM Academy likely offers courses, workshops, or resources to educate individuals on how to effectively utilize the software for analyzing by explaining mathematics of the governing equations involved in various simulation tools for all different types of analysis, enroll for our FEA courses such as Ansys course in India – explore more by visiting our website http://www.artem.co.in.