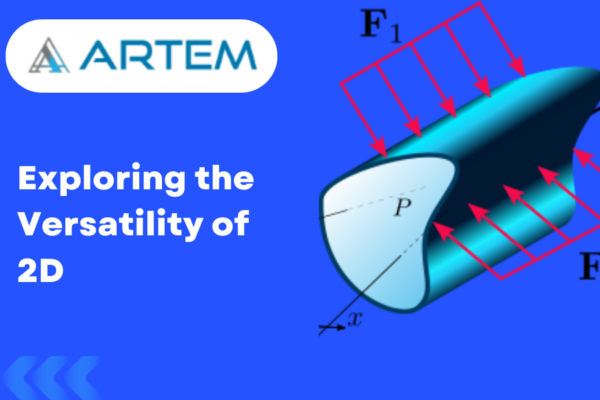
Exploring the Foundations: Assumptions of Linear Static Analysis in Engineering
Linear static analysis makes several assumptions to simplify the analysis of structures. These assumptions are necessary to apply the principles of linear elasticity and simplify the governing equations. Here are some common assumptions made in linear static analysis:
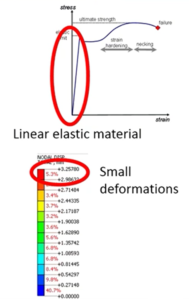
Linear Elastic Material Behavior: Linear static analysis assumes that the material used in the structure exhibits linear elastic behavior. This means that the material obeys Hooke’s law, where the stress is directly proportional to the strain within the elastic limit. Nonlinear material behavior such as plasticity, creep, or large deformations is not considered in linear static analysis.
Small Deformations: Linear static analysis assumes that the deformations in the structure are small. This assumption allows the use of the linear strain-displacement relationship, where the strain is directly proportional to the displacement. Large displacements that cause significant geometric changes and nonlinear effects are not considered in linear static analysis.
Linear Relationship between Loads and Displacements: Linear static analysis assumes that the applied loads and resulting displacements have a linear relationship. This assumption implies that the structure’s response is directly proportional to the applied loads. It assumes that the superposition principle holds, meaning the response to multiple loads is the sum of the individual responses to each load.
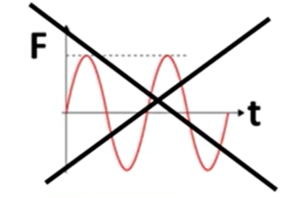

Static Equilibrium: Linear static analysis assumes that the structure is in a state of static equilibrium. This means that the applied loads and internal forces within the structure are balanced, resulting in zero net force and moment. Dynamic effects, such as inertial forces, are not considered in linear static analysis.
Homogeneous and Isotropic Material: Linear static analysis assumes that the material properties of the structure are homogeneous (uniform throughout) and isotropic (properties do not vary with direction). This simplifies the analysis by assuming that the material behaves the same in all directions.
Small Strain Theory: Linear static analysis employs the small strain theory, which assumes that the strains in the structure are small enough that the change in shape can be approximated by linear relationships. By making this assumption, the strain-displacement equations become simplified, facilitating the analysis process.
At Artem Academy, we offer a comprehensive ANSYS course that covers the principles and applications of finite element analysis. Our course delves into various aspects of structural analysis, including linear static analysis. For more details, advanced analysis techniques, such as nonlinear analysis, may be required to accurately model the behavior of the structure .By enrolling in our ANSYS course online, students will gain a solid understanding of how to effectively utilize the ANSYS software to perform linear static analysis and other advanced simulations.
Throughout the course, we explore the limitations of this theory and introduce more advanced analysis methods for scenarios where large strains or nonlinear behavior are involved. By providing a well-rounded education in structural analysis, our ANSYS course equips students with the necessary knowledge and skills to tackle complex engineering challenges.
Whether you are a beginner seeking an introduction to ANSYS or an experienced professional looking to enhance your simulation capabilities, Artem Academy’s ANSYS course is designed to meet your needs. Join us today and take your engineering analysis skills to new heights.