Mastering Free-Free Modal Analysis: Formulation, Principles, and Applications
In the realm of structural engineering, the quest for understanding the dynamic behavior of systems has led to the development of sophisticated analysis techniques. One such powerful method is Free-Free Modal Analysis, a process that goes beyond conventional modal analysis by considering structures that are unrestrained at their boundaries. In this blog, we’ll explore the formulation behind Free-Free Modal Analysis, unlocking the secrets to finding natural frequencies and mode shapes.
Understanding the Basics:
Before delving into the formulation, let’s grasp the fundamental principles governing Free-Free Modal Analysis:
- Unrestrained Boundaries: Unlike traditional modal analysis, Free-Free Modal Analysis assumes that the structure is not fixed or constrained at its boundaries. This is a crucial departure from other modal analysis methods, as it allows for a more accurate representation of the dynamic behavior of the system.
- Natural Frequencies: The primary objective of this analysis is to determine the natural frequencies of the structure. These frequencies represent the inherent vibrational modes of the system and are critical for understanding how it responds to dynamic loads.
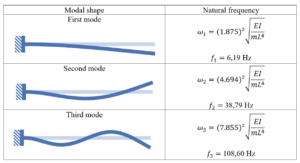
- Mode Shapes: Mode shapes describe the spatial distribution of deformations within the structure during vibration. Identifying mode shapes is essential for gaining insights into the dynamic response and potential weaknesses of the system.
Formulation of Free-Free Modal Analysis:
The formulation for Free-Free Modal Analysis involves solving the equations of motion for the structure. The basic equation of motion for a single-degree-of-freedom system can be expressed as:
M is the mass matrix,
C is the damping matrix,
K is the stiffness matrix,
u is the displacement vector,
¨u¨ is the acceleration vector,
˙u˙ is the velocity vector, and
F is the force vector.
For a structure with multiple degrees of freedom, the equation of motion becomes a set of coupled second-order differential equations, typically represented in matrix form as:
$$M\ddot U+\;C\dot U+\;KU\;=F$$
where U is the vector of displacements for all degrees of freedom.
To find the natural frequencies and mode shapes, one needs to solve the eigenvalue problem:
$$2KU=\omega2MU$$
Here,
ω represents the circular frequency, and
U is the eigenvector associated with each natural frequency.
Once the natural frequencies (ω) are obtained, the corresponding mode shapes can be extracted from the eigenvectors U. These mode shapes depict the spatial distribution of deformations during vibration.
Applications and Benefits:
- Aerospace Industry: Free-Free Modal Analysis aids in optimizing the design of aircraft and spacecraft, ensuring that the structures can withstand dynamic loads encountered during flight.
- Automotive Engineering: In the automotive sector, this analysis technique is employed to enhance vehicle safety, comfort, and overall performance by identifying and addressing potential vibration issues.
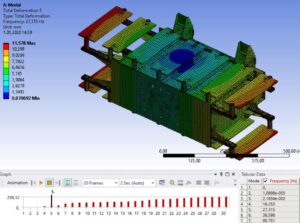Civil Engineering: Free-Free Modal Analysis plays a crucial role in designing resilient structures such as bridges and buildings, helping engineers understand and mitigate the impact of dynamic forces like wind and earthquakes.
Conclusion:
Free-Free Modal Analysis, with its sophisticated formulation, stands as a cornerstone in unraveling the complexities of structural dynamics. Armed with the ability to determine natural frequencies and mode shapes, engineers can optimize designs and ensure the robustness of structures across various industries. As technology advances, the integration of such analytical tools continues to shape the future of structural engineering, offering unprecedented insights for safer and more efficient designs.
