Essential Concepts in Modal Analysis: Mode Shapes and Nodal Diameters
In modal analysis, mode shapes and nodal diameters are essential concepts that provide valuable insights into the dynamic behavior of structures. Let’s delve into each term and understand their significance, along with the corresponding formulas.
Mode Shapes:
Definition: Mode shapes represent the spatial distribution of displacements within a structure at a specific natural frequency. They illustrate how different parts of the structure move relative to each other during vibration.
Formula: For a structure with n degrees of freedom, the mode shape is represented by a vector U, where each element Ui denotes the displacement at the i-th degree of freedom.
The mode shape is obtained by solving the eigenvalue problem:
$$=2KU=\omega2MU$$
- K is the stiffness matrix,
- M is the mass matrix,
- ω is the circular frequency (related to the natural frequency by =2 ω=2πf),
- U is the mode shape vector.
In practical terms, once the eigenvalues and eigenvectors are obtained, the mode shapes are extracted from the eigenvectors.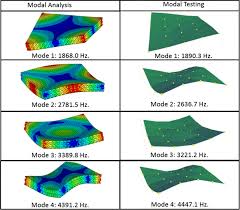
Nodal Diameters:
Definition: Nodal diameters are regions within a mode shape where the displacement is zero. These nodal diameters correspond to points of minimal or no movement during vibration.
Formula: The nodal diameters can be understood through the mode shape vector U. The positions where the elements of U are zero represent nodal points or lines. For a given mode shape, the nodal diameters are essentially the areas or lines of the structure where no motion occurs.
For a 1D structure (e.g., a beam), a nodal diameter might be a point where the displacement is zero. For a 2D structure (e.g., a plate), nodal diameters could be lines or curves where the displacement is zero. In 3D structures, nodal volumes may exist.
Significance:
- Mode Shapes: Understanding mode shapes is crucial for engineers as they provide a visual representation of how a structure deforms during vibration. This insight is essential for optimizing designs, identifying potential weaknesses, and ensuring that the structure can withstand dynamic loads without encountering resonance issues.
- Nodal Diameters: Identifying nodal diameters helps engineers pinpoint regions in a structure where minimal or no movement occurs during vibration. This information is valuable for design optimization, allowing engineers to reinforce or modify specific areas to enhance structural performance.
In summary, mode shapes and nodal diameters play pivotal roles in modal analysis, offering engineers a deeper understanding of the dynamic response of structures and aiding in the design and optimization processes.