Types Of Non-Linearity
Nonlinearity is natural in physical problems. In fact, the linear assumptions we make are only valid in special circumstances and usually involve some measure of “smallness”, for example, small strains, small displacements, small rotations, small changes in temperature, and so on.
We use linear approximations not because they are more correct but because
Linear solutions are easier to compute.
The computational cost is smaller.
Solutions can be superposed on each other
A nonlinear analysis is needed if the loading on a structure causes significant changes in stiffness. Typical reasons for stiffness to change significantly are:
⁻ Contact between two bodies
⁻ Strains beyond the elastic limit (plasticity)
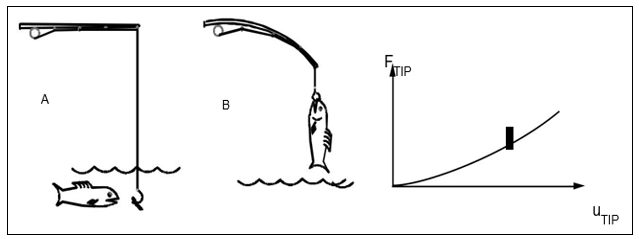
⁻ Large deflections, such as with a loaded fishing rod
However, linear analysis is not adequate and nonlinear analysis is necessary when
Designing high-performance components
Establishing the causes of failure
Simulating true material behavior
Trying to gain a better understanding of physical phenomena
Modern analysis software makes it possible to obtain solutions to nonlinear problems. However, experienced skill is required to determine their validity and these analyses can easily be inappropriate. Care should be taken to specify appropriate model and solution parameters. Understanding the problem, the role played by these parameters and a planned and logical approach will do much to ensure a successful solution.
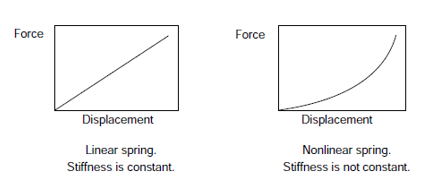
Generally, linear analysis means that the relationship between the applied force and the response to this force (Ex: displacement) is linear in nature. We know that this displacement can be obtained by inverting the stiffness matrix and then multiplying it with the force vectors. In other words, this means that the stiffness matrix does not change during a linear analysis.
This can be further emphasized by taking the example of spring with linear and nonlinear characteristics.
As the stiffness is dependent on the displacement, which keeps changing, the initial stiffness matrix cannot be used without continually updating and inverting it during the course of the analysis. This is the reason why nonlinear analysis takes more time to solve compared to linear FEM analysis.
Mostly, nonlinear analysis depends on the need of the goals i.e., for fatigue, dynamic and so on. A cost-benefit analysis is usually necessary before embarking on the nonlinear analysis of a problem.
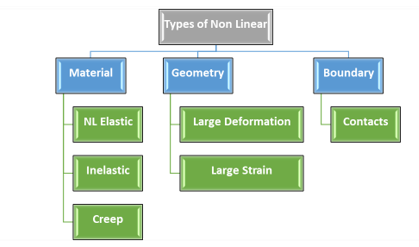
There are three major types of non-linearity:
Material (plasticity, creep, viscoplasticity/viscoelasticity)
Geometric (large deformation, large strains)
Boundary
These may occur singly or in combination.
Material Non-linearity:
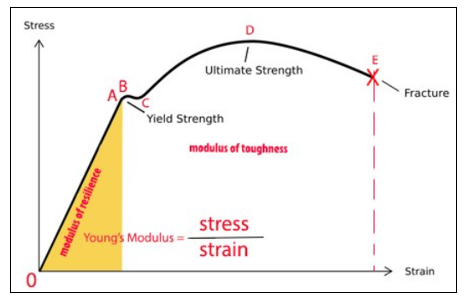
Nonlinear stress-strain relationships are a common cause of nonlinear structural behaviour. Material nonlinearity involves the nonlinear behavior of a material based on a current deformation, deformation history, rate of deformation, temperature, pressure, and so on. Examples of nonlinear material models are large strain (Visco) elasto-plasticity and hyperelasticity (rubber and plastic materials) and other types.
Many factors can influence a material’s stress-strain properties, such as:
Load history (as in elastoplastic response)
Environmental conditions (such as temperature)
The amount of time that a load is applied (as in creep response)
Geometric Non-linearity
Geometric nonlinearity arises when the changes in the model’s geometry are very high during the course of deformation. This happens when there are
Large deformations
Large rotations
Both
Initial loading conditions before the start of the analysis
If a structure experiences large deformations, its changing geometric configuration can cause the structure to respond nonlinearly
Geometric nonlinearity is characterized by “large” displacements and/or rotations
In linear geometric analysis, the deformations and rotations are smaller like within 5 % as a generic rule, but in the case of nonlinear geometric analysis, displacement and rotations are large. Small changes in the magnitude of force for nonlinear geometry, can change convergence behavior considerably. However, the geometric nonlinearity is not only due to large deformation/rotation but varies based on loading and situation too.
An example would be the fishing rod
It is difficult to predict the case of geometric nonlinearity, as it needs a lot of experiments and judging the case by looking at the scenario. In FEA software geometry nonlinear is solved simply by keeping the nonlinear zone on.
In analyses involving geometric nonlinearity, changes in geometry as the structure deforms are considered in formulating the constitutive and equilibrium equations. Many engineering applications such as metal forming, tire analysis, and medical device analysis require the use of large deformation analysis based on geometric nonlinearity. Small deformation analysis based on geometric nonlinearity is required for some applications, like analysis involving cables, arches and shells.
Contact non-linearity:
When two separate surfaces touch each other such that they become mutually tangent, they are said to be in Contact. In contact nonlinearity, abrupt change in stiffness may occur when bodies come into or out of contact with each other. This type of nonlinearity is used to simulate the gap between two parts.
In the common physical sense, surfaces that are in contact have the below characteristics:
They do not interpenetrate
They can transmit compressive normal forces and tangential friction forces
They often do not transmit tensile normal forces
They are therefore free to separate and move away from each other

Nonlinear FEA Issues:
Achieving convergence: Obtaining convergence is the biggest challenge in nonlinear analysis.
Trial and error are sometimes required.
Complex problems might require more load increments, and many iterations at each load step to achieve the convergence.
Balancing expenses versus accuracy
FEA involves expenses (Solution time, disk and memory requirements)
More detail and a finer mesh generally lead to a more accurate solution but require more time and system resources.
Nonlinear analysis needs additional iteration that affects both accuracy and expenses.
Verification
Difficult to verify the FEA results due to the increased complexity of nonlinear behaviour.
The sensitivity studies (mesh convergence, increased mesh density, reduced load increments, varying other model parameters) become more expensive.
Results of the nonlinear analysis cannot be scaled.
The structural behavior can be markedly non-proportional to the applied load.