Shear Force And Bending Moment
Shear Force and Bending Moment
The two terms hold great significance in Solid Mechanics and Engineering Mechanics. These concepts are the foundation of theories in Solid Mechanics. Thus, one needs to carefully understand these areas. Shear Force Diagram (SFD) and Bending Moment Diagrams (BMD) are analytical tools used to perform structural design. For example, A Beam is defined as a structural member subjected to transverse shear loads during its functionality. Due to those transverse shear loads, beams are subjected to variable shear force and variable bending moment. These diagrams can be used to easily determine the type, size, and material of a member in a structure to support loads without structural failure. Another application of shear and moment diagrams is that the deflection of a beam can be easily determined.
SHEAR FORCE:
The net effect of the shear force is to shear off the beam along with the point at which it is acting. In other words, the force acts perpendicular to the body and tries to push one part of the body and one part in another direction. The force always acts tangential to the surface.
Shear Force at a cross-section of the beam is the sum of all vertical forces either at the left side or at the right side of that cross-section. Shear force is taken +ve if it produces a clockwise moment and it is taken -ve when it produces an anti-clockwise moment.
Force acting on the right-hand side of the section in the upward direction is taken –ve, the force acting on the right-hand side of the section in the downward direction is taken +ve. SFD is the graphical representation of the variation of shear force along the length of the beam.

A shear force diagram shows the shear force at every section of the beam due to transverse loading on it. Its baseline is equal to the span of the beam, drawn on a suitable scale.
For point loads S.F.diagram has a straight horizontal line, for UDL, it has straight inclines lines, and for uniformly varying loads it has a parabolic curve.
Bending Moment: – The moment of the force and the distance about which the tendency of rotation is observed is known as the Bending Moment. This is specifically referred for beams or any other structural elements.
The bending moment at a cross-section of the beam is the sum of all the moments either at the left side or at the right side of that cross-section. First of all, remove all the loads and reactions from any one side of the section. Now introduce each load and reaction one at a time and find its effect in the section.
BMD is the graphical representation of the variation of bending moment along the length of the beam
BMD that causes concavity upwards is taken as +ve called sagging and BMD that causes convexity upwards is taken as -ve called hogging

Practical Example
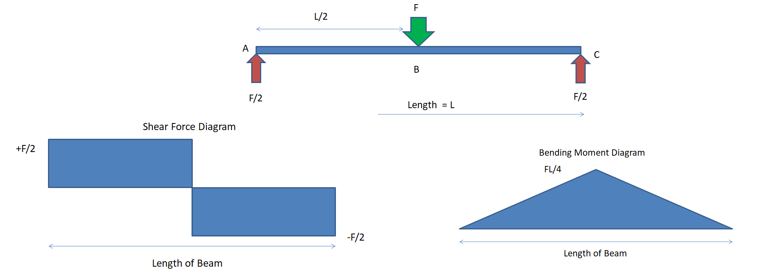
Consider a simply supported beam of length L and force F at the center of the structural beam, as shown in Fig 1 below. Check for SFD and BMD figures along with derivation show to get the reaction results.
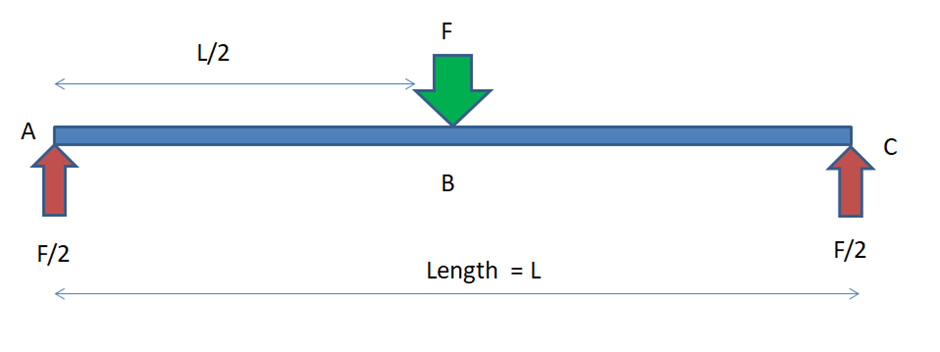
Fig. 1: Simply Supported Beam with a point Load
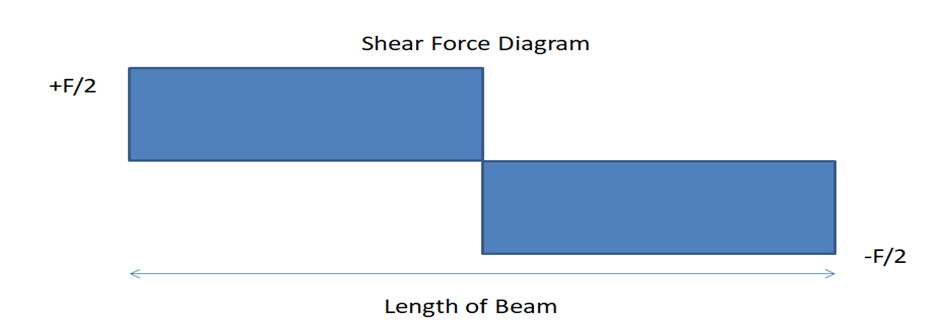

Fig. 2 Shear Force and Bending Moment diagram for the point Load application
A bending moment diagram is a diagram that shows the bending moment at every section of the beam due to transverse loading on it.
In the case of simply supported beam bending moment is zero at the ends, and for a cantilever, it is zero at the free end. For point loads, the B.M. diagram has straight inclined lines, for UDL, it has a parabolic curve and for the uniformly varying load, it has a cubic curve.
Equations for the above beam are shown in Figure 1
Consider the two reactions and the following equations
The variations of SFD and BMD can be seen in Fig. 2
The F Force that can be seen in Fig 1. is the shear force, as it is trying to put a tangential load. The side arrows represent the reaction forces. The above fig
Force Balance:
Taking Moment about A:
Calculation of Reactions:
Force varying in Section B – C:
Moment varying in Section B – C:
Force varying in Section A – B:
Moment varying in Section A – B:
The variations of SFD and BMD can be seen in Fig. 2
The F Force that can be seen in Fig 1. is the shear force, as it is trying to put a tangential load. The side arrows represent the reaction forces. The above figure is called a SIMPLY SUPPORTED BEAM, one of the most used cases in Solid mechanics.
2. practical Example :
In this we are considering only the moment at the center of the beam, to see how the effect varies in reaction moments and forces. The length of the beam is considered as L and the moment at the center as M.
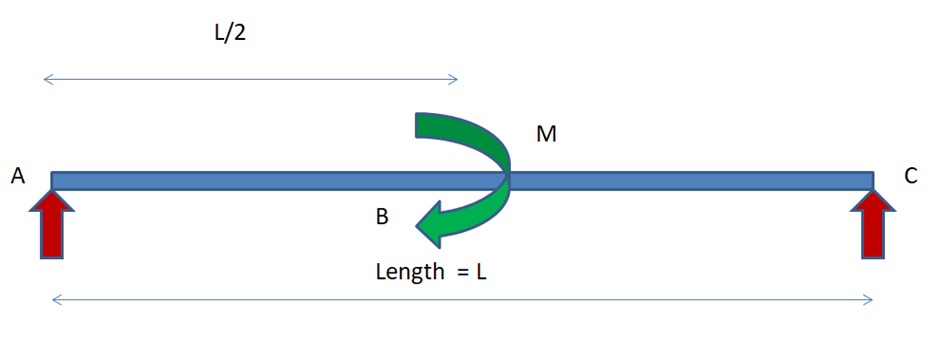
Fig. 3: Simply Supported Beam with a Moment acting at center

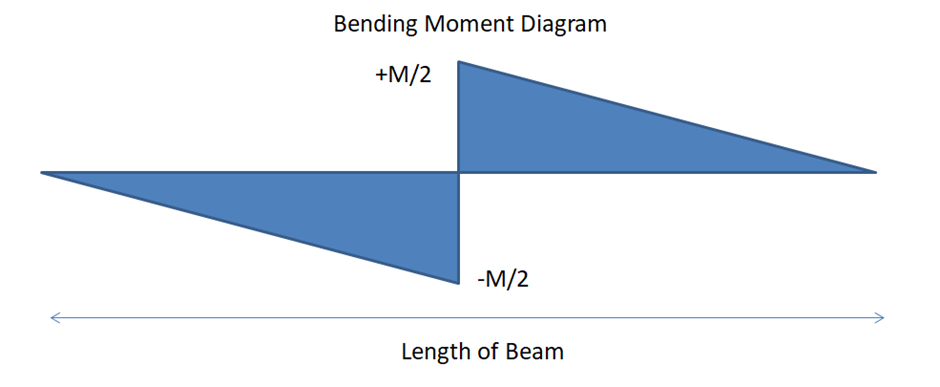
Fig. 4: Shear Force and Bending Moment for the application of Moment
Force Balance:
Taking Moment about A:
Calculation of Reactions: ,
Force varying in Section B – C:
Moment varying in Section B – C:
Force varying in Section A – B:
Moment varying in Section A – B:
Fig. 3 represents a simple example in which moment has been applied on the simply supported beam. The Magnitude of the moment has been assumed to be M, and on calculations, we would reaction forces as well.
Fig. 4 represents the Bending Moment Diagram of the above example. One observation that can be made from the figure is that after the application of the moment there is the spike in the Bending Moment Diagram of Fig. 3, whereas there can be seen no so such spike as in the case of Fig. 3 Bending Moment Diagram.
Finally to conclude, from these examples is that whenever there is a concentrated moment on a beam a spike would be observed. The same analogy can be used for the Shear Force Diagram in example 1. A sudden spike in Shear Force Diagram can be observed because of a concentrated point load.
POINTS TO PONDER
- Shear Force Acts Tangentially to the surface.
- Sudden Spike can be seen in Shear Force Diagram with the application of point force
- Consider either left or right-hand side of the section
- SFD will decrease or increase suddenly due to vertical point load
- Add Forces normal to the beam on one side. For Eg: the right-hand side is chosen, the force acting downwards is +ve and the force acting upwards is –ve
- SF between any 2 vertical loads are constant and represented as horizontal
- A sudden spike can be seen in Bending Moment Diagram with an application of the concentrated moment.
- The +ve values of SFD & BMD have plotted above and -ve values below the baseline
- BM at the 2 supports of a simply supported beam & also at the free end of a cantilever will be zero